Petra on Programming: Truncated Indicators

Cumulative indicators, such as the EMA or the MACD, are affected by a theoretically infinite history of candles. In finite backtests, these indicators return slightly different results depending on the test period. This effect is often assumed negligible. But John Ehlers demonstrated in his July S&C article that it is not so. At least not for some indicators, such as a narrow bandpass filter. We have to truncate the indicator’s ‘internal history’ for getting consistent results. How do we do that in C?

Bandpass filters are normally used for detecting cycles in price curves. But they do not work well with steep edges in the curve. Sudden price jumps cause a narrow-band filter to ‘ring like a bell’ and generate artificial cycles that can cause false triggers. As a solution, Ehlers proposed to truncate the candle history of the filter. Limiting the history to 10 bars effectively dampened the filter output and produced a better representation of the cycles in the price curve.

For limiting the history of a cumulative indicator, we’re not using Ehler’s code here, but write a general ‘truncate’ function that works for any indicator:

var indicator(vars Data,int Period,var Param);

var truncate(function Indicator,vars Data,int Period,var Param)
{
 indicator = Indicator;
 var *Trunc = zalloc(UnstablePeriod*sizeof(var));
 var Ret;
 int i;
 for(i = UnstablePeriod-1; i >= 0; i--) {
   SeriesBuffer = Trunc;
   Ret = indicator(Data+i,Period,Param);
   shift(Trunc,0,UnstablePeriod);
 }
 return Ret;
}

This function accesses the internal data series of the cumulative indicator which is passed as the first argument. The SeriesBuffer variable replaces that series with an external array that’s temporarily allocated on the C heap with the zalloc function. UnstablePeriod is a global variable already used by Zorro for limiting the history range of traditional indicators, such as EMA or MACD. The truncate function returns the value of the truncated indicator.

The following code shows how the truncate function is used with our narrow bandpass filter:

function run()
{
 BarPeriod = 1440;
 StartDate = 20181101;
 assetAdd("SPY","STOOQ:SPY.US"); // load price history from Stooq
 asset("SPY");
 UnstablePeriod = 10;
 vars Prices = series(priceClose());
 var PB = BandPass(Prices, 20, 0.1);
 var Trunc = truncate(BandPass, Prices, 20, 0.1);
 plot("Bandpass",BP,NEW|LINE,RED);
 plot("Truncated",Trunc,LINE,BLUE);
}

Applied to SPY:

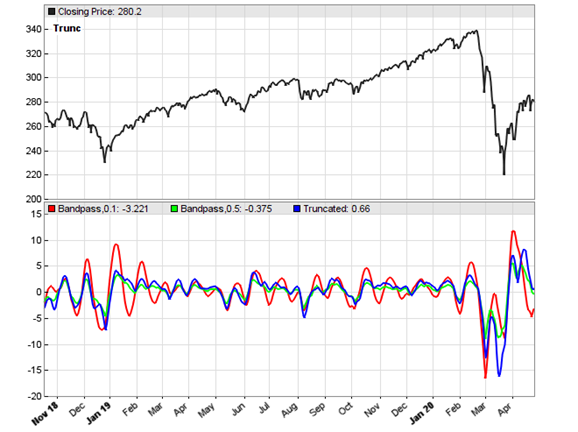
The chart confirms Ehler’s observation that the truncated narrow bandpass (blue line) represents cycles better than the original bandpass (red line). For comparison I’ve added a medium-wide bandpass filter as it’s normally used in trading systems (green line). This filter doesn’t ‘ring’ either, truncated or not. This makes me wonder: What is the better choice for detecting cycles, a truncated narrow bandpass or simply a non-truncated wide bandpass?

For finding out, we feed the three bandpass variants with a sine chirp and compare their responses. The resulting charts:

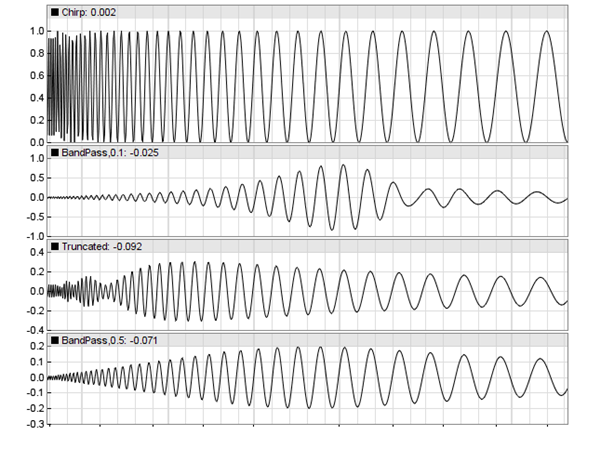
The top chart is the chirp, a sine wave with a period rising from 5 to 60 cycles. The charts below show the chirp responses of the original narrow bandpass, the truncated narrow bandpass, and the wide bandpass. And here we can see that truncation produced strange artifacts: the bandpass got a wider bandwidth, some wiggles at the low cycles, and a shifted center frequency. A nontruncated filter with an already wider bandwidth seems here the clearly better solution.

I think you should not truncate a filter to just 10 bars. The ta-lib used by Zorro truncates indicators to 40 bars by default, and affects only classical indicators such as EMA. The advantage of proper truncating is that the indicator output does not depend on the previous history and lookback period of the trading system. A disadvantage is speed: truncating makes indicators much slower because they run in a loop. Not very relevant for normal trading systems, but for HFT systems.

The truncate function and the test scripts can be downloaded from the 2020 script repository. Zorro 2.28 or above is required.